在单体量子力学的问题中,定态薛定谔方程可以被转换为SL问题,系统的本征态可以通过各种复杂的特殊函数表示描写。如果系统具有的是简单的离散自由度$\vert m\rangle$(例如自旋),那么我们可以将系统的状态通过不同的离散模式来进行描写,即单体粒子是处于什么模式状态。
从单体变成多体,系统的复杂程度将面临指数爆炸。描述每个粒子所处的状态变得困难,然而如果构成系统的微观粒子具有全同性,我们就可以转换视角,从系统模式的角度进行描述。即描述系统的状态等价于描述清楚每个模式占据的粒子数。这样的视角同样适用于可分辨粒子系统(例如自旋系统),描述清楚每个自旋的状态与描述清楚每个模式的占据状态存在着一一对应。
在多体物理的视角下,系统整体的希尔伯特空间具有以下的结构:
\[\mathcal{H} = \mathcal{H}_1\otimes \mathcal{H}_2\otimes \mathcal{H}_3\otimes ...\]即它是一系列局域希尔伯特空间的张量积。系统的本征态则可以通过这些局域希尔伯特空间的直积态进行展开:
\[\vert \psi\rangle = \sum_{\{s_n\}}C[s_1,s_2,s_3,...] \vert s_{1}, s_{2}, s_3,... \rangle\]其中叠加系数张量$C[s_1,s_2,s_3,…]$可以通过一系列的SVD分解来实现所谓的Tensor-Train分解,在分解后具有以下形式:
\[\vert \psi\rangle = \sum_{\{s_n\}}\sum_{\alpha\beta\gamma...} A^1_{\alpha\beta}[s_1]A^2_{\beta\gamma}[s_2] A^3_{\gamma...}[s_3]...\vert s_1,s_2,s_3,...\rangle\]分解得到的具有这样形式的波函数被称作是MPS。
一个非常重要的问题是去询问:这些分解得到的张量$A^i_{\alpha\beta}[s_i]$,它们的物理含义是什么?
Schmidt分解
考虑系统可以被分成两个子系统$A,B$,子系统A可以通过基矢量${\vert a\rangle}$完备描述,而子系统B则可以通过${\vert b\rangle}$得到完备描述,系统的基矢量则是${\vert a\rangle_A\vert b\rangle_B}$。
系统的一个一般量子态可以表达成:
\[\vert \psi\rangle =\sum_{a,b}C_{a,b}\vert a\rangle_A\vert b\rangle_B\]可以对矩阵$C_{a,b}$进行SVD分解:
\[C_{a,b} =\sum_{\lambda} U_{a,\lambda} S_\lambda V_{\lambda, b}\]从而量子态可以被表达成:
\[\vert \psi\rangle = \sum_{\lambda}S_\lambda \vert \lambda\rangle_A \vert \lambda\rangle_B\]其中有:
\[\vert \lambda\rangle_A = \sum_a U_{a,\lambda}\vert a\rangle_A, \ \ \ \vert \lambda\rangle_B = \sum_b V_{\lambda,b} \vert b\rangle_B\]这就是所谓的Schmidt分解,它告诉我们一个很重要的信息,即在原来的表象下描述系统,我们需要$\dim(A)\times \dim(B)$数量的参数,但这些参数中存在着关联,实际上独立的参数只有$\min{\dim(A),\dim(B)}$。这背后所反映的物理是:通过理解两个子系统之间的纠缠,我们就可以理解系统整体的行为。
从Schmidt分解到Tensor-Train,再到Tensor Network
通过Schmidt分解我们看到,每一个局域张量$A^i_{\alpha\beta}[s_i]$刻画了局域模式/局域希尔伯特空间$\mathcal{H}_i$与周围环境的纠缠。对于Tensor-Train或者开边界的MPS,把局域模式/格点$i$去除后得到的环境可以被区分成两个独立的部分:左环境和右环境。
具体而言,分别进行其他局域张量的缩并,我们可以得到:
\[\vert \Phi^{[1:i-1]}_{L,\alpha}\rangle = \sum_{\gamma\eta...}A^{1}_{\gamma\eta}[s_1] A^2_{\eta...}[s_2]...A^{i-1}_{...\alpha}[s_{i-1}]\vert s_1,s_2,...,s_{i-1}\rangle\] \[\vert \Phi_{R,\beta}^{[i+1:N]}\rangle = \sum_{\gamma\eta...}A^{i+1}_{\beta\gamma}[s_{i+1}]A^{i+2}_{\gamma\eta}[s_{i+2}]...\vert s_{i+1},s_{i+2},...\rangle\]这样系统的波函数就可以在局域格点的表象下进行展开:
\[\vert \Psi\rangle = \sum_{\alpha,s_i,\beta}A^i_{\alpha\beta}[s_i] \vert \Phi_{L,\alpha}^{[1:i-1]}\rangle \vert s_i\rangle \vert \Phi^{[i+1:N]}_{R,\beta}\rangle\]局域张量$A^i_{\alpha\beta}[s_i]$即局域模式/格点表象下的波函数。
可以去问这样一个问题:难道仅需要了解局域模式/格点下的波函数就可以知道真个系统的行为了吗?当然不是,我们还需要知道对应的环境纠缠的基矢$\vert \Phi^{[1:i-1]}_{L,\alpha}\rangle\vert \Phi_{R,\beta}^{[i+1:N]}\rangle$,而一个看起来不太平凡的事实是知道所有其他局域格点表象下的波函数就知道了环境的纠缠基矢
波函数具有规范自由度,其性质深刻地反映在了局域张量的规范变换中。我们对局域基底$\vert s_i\rangle$进行规范变换$U[s_i]^\dagger\vert s_i\rangle$,对应的波函数/局域张量也要进行相应的变换$\sum_{s_i} A^i_{\alpha\beta}[s_i]U[s_i]$
我们也可以对环境基底进行规范变换,相应地局域张量会经历对应的规范变换:$A^i[s_i]\mapsto A^i_G[s_i] = G^{-1}(i-1)A^i[s_i] G(i)$
由于Tensor-Train/MPS结构的特殊性,我们可以找到所谓的“正则条件”来固定局域张量在环境基底上的规范自由度。其含义为左右的环境基底各自构成对应的正交基底。(如图所示,图片来源:PhysRevB.94.165116)
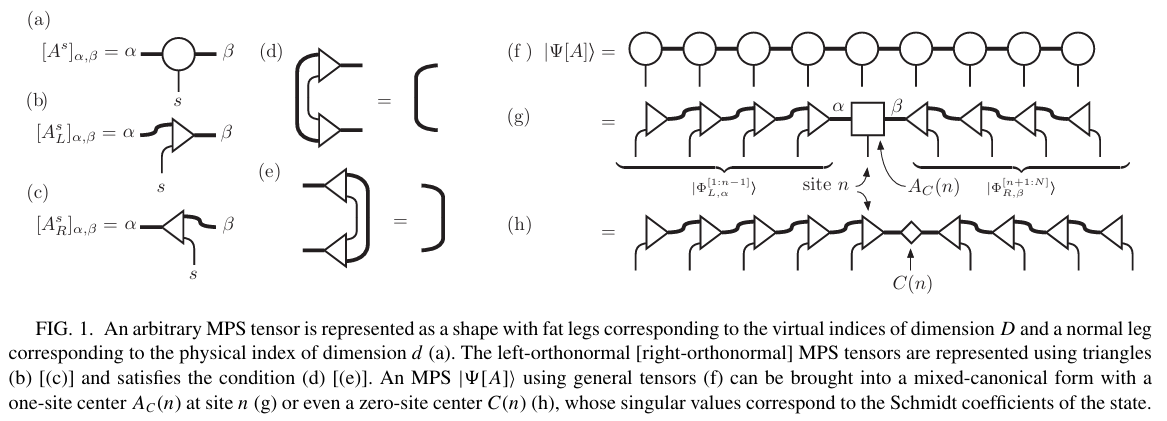
我们也可以把局域模式$i$吸收到一个环境中,这样就转变成了Schmidt分解所处理的两个子系统的情况。例如将模式$i$吸收到左环境中得到$\vert\Phi_{L,\alpha}^{[1:i]}\rangle=\vert\Phi_{L,\alpha}^{[1:i-1]}\rangle\vert s_i\rangle$,在程序上即把张量元的指标$\alpha, s_i$进行group操作。
局域空间的投影算符
自动微分
